
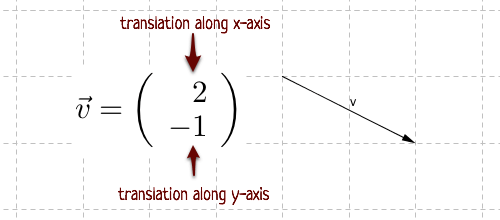
However, it is useful in higher dimensions as well. The motion or changes in shape of an object moving in the plane or in 3-space. This geometric point of view is obviously useful when we want to model Transformation, but there is a simple and useful trick that allows us to Have our robot walk across the room or we may want to slide a figure toĪ new position on the computer screen. Transformations and translations as well. In both these applications we probably need three dimensional Linear transformationsĪnd matrices are also an important tool if we want to control the motion Will make it appear to move away from the viewer.

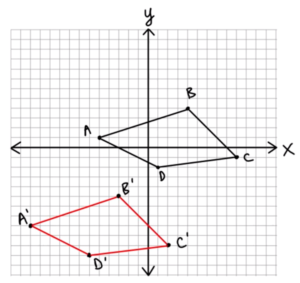
Motion effects canīe achieved as well as a simple example, shrinking an object Then projections and rotations come into play. If for example we need to represent a 3-dimensional object on a 2-dimensionalĬomputer screen and we want to look at the object from various angles, Such as rotation, stretching, shrinking, shearing and projection.Īs a consequence linear transformations are important in computer graphics. It turns out thatĪll linear transformations are built by combining simple geometric processes If we start with a figure in the xy-plane, then we can apply theįunction T to get a transformed figure. = (ax + by, cx + dy) where a,b,c and d are real numbers. A linear transformation on the plane is a function of the form T(x,y)


 0 kommentar(er)
0 kommentar(er)
